Flaming

PENGERTIAN FLAMING

DAN

ANALISIS KASUS FLAMING

OLEH :

Devita Nurul Aulia                 11515768

Regina Aprioni Iraswari          15515722

Syifa Rahma Ismira                16515785

Tria Luvita Dewi                    17515692

  

PSIKOLOGI

UNIVERSITAS GUNADARMA

2016

BAB I

PENDAHULUAN

1.1   Pengertian Flaming

Flaming adalah teknik pelecehan yang pengganggu sering digunakan dalam berbagai forum online. Flaming juga terjadi di situs sosial media, blog pribadi, chat room, kelompok email dan situs video terkenal seperti YouTube. Bullies sering menggunakan Internet untuk mengintimidasi, menghina dan membingungkan orang karena mereka tidak harus mengungkapkan identitas mereka untuk melakukan seperti itu. Anak-anak yang menggunakan Internet untuk browsing atau melakukan studi rentan untuk memiliki berjalan-in dengan orang-orang ini, yang sering disebut sebagai cyber bully. Flaming adalah salah satu dari lima taktik pelecehan yang pengganggu gunakan untuk menyiksa korban-korban mereka.

Flaming adalah kata lain untuk versi tertulis dari pelecehan verbal, emosional dan bahkan seksual. Flamer menulis konten yang akan memanggil emosi tertentu dan tanggapan seperti kemarahan, kesedihan, penghinaan, keraguan diri dan lebih. Beberapa flamers mencari orang-orang yang antusias tentang mata pelajaran tertentu, dan mereka sengaja menampar subjek. Beberapa flamers sengaja mulai argumen tentang topik apapun. Sebagian besar waktu, mereka tidak memiliki alasan yang sah untuk berdebat, dan mereka akan sering mendapatkan defensif kalau ada yang menantang api mereka. Email kedua atau komentar dari Flamer biasanya melibatkan senonoh dan penghinaan pribadi. Flamer dapat meletakkan ras, jenis kelamin, orientasi seksual, status ekonomi seseorang dan masih banyak lagi. Banyak flamers memangsa pengguna internet yang tampaknya rentan. Jika Flamer dapat mengetahui informasi pribadi tentang target, maka ia akan menggunakannya untuk menyebabkan orang kesusahan tambahan. Siapapun bisa menjadi korban pengganggu yang api. Mereka akan mencoba untuk menyerang siapa saja yang menghabiskan waktu di dunia internet. Negatif bahan bakar reaksi Flamers paling karena mereka tahu bahwa mereka telah marah orang lain. Intent mereka adalah untuk melampiaskan malapetaka di kehidupan orang-orang yang tidak bersalah.

1.2   Tujuan Pencantuman Pengertian Flaming

-          - Untuk mengetahui definisi Flaming secara lengkap dan jelas.

-          - Untuk mempermudah proses pengerjaan tugas softskill.

BAB II

CONTOH KASUS

BAB III

ANALISA

Sesuai contoh kasus di atas yang tersebar di media, pemberitaan mengenai hubungan raffi ahmad dan ayu ting-ting semakin lama semakin menjadi buah bibir dimasyarakat. Namun, banyak masyarakat yang mengomentari dengan mencibir disosial media dengan bahasa kasar sampai membandingkan ayu ting-ting dan nagita slavina. Akun-akun haters yang tersebar di media sosial berupaya untuk menjatuhkan ayu ting-ting dengan mengajak orang lain membencinya. Haters tak hentinya menghujat ayu ting-ting di media sosial karena semakin banyak haters  yang menyebarkan postingan-postingan yang mengandung penghinaan dan lain-lain. Padahal, belum tentu apa yang mereka komentari adalah hal yang sebenarnya. Dan sampai saat ini ayu maupun rafi belum mengkonfirmasi berita yang tersebar ini.

Sumber:

cyberbullying.com

instagram.com/boikotayutingting_

Peranan Psikologi Industri dan Organisasi

Psikologi Industri dan Organisasi merupakan suatu keseluruhan pengetahuan yang berisi fakta, aturan dan prinsip perilaku manusia pada pekerjaan.
Psikologi industri dan organisasi adalah ilmu yang mempelajari manusia baik secara perorangan maupun secara kelompok, dengan maksud agar temuannya dapat diterapkan dalam industri dan organisasi untuk kepentingan dan kemanfataan manusianya dan organisasinya selain itu juga berperan sebagai tenaga kerja dan sebagai konsumen.
Jadi, peran psikologi industri dan organisasi dalam bidang industri sangat penting terutama dalam bidang pengembangan SDM karena berhubungan langsung dengan individu dalam memilih tenaga kerja yang tepat untuk perusahaan.

Devita Nurul Aulia
2PA10
11515768

Proposisi

Ilmu Alamiah Dasar

Oleh :

Devita Nurul Aulia (11515768)

1 PA 03

Universitas Gunadarma

BAB 1

PENDAHULUAN

1.1 Latar Belakang

Proposisi adalah istilah yang digunakan untuk kalimat pernyataan yang memiliki arti penuh dan utuh. Hal ini berarti suatu kalimat harus dapat dipercaya, disangsikan, disangkal, atau dibuktikan benar tidaknya. Singkatnya, proposisi adalah pernyataan mengenai hal-hal yang dapat dinilai benar atau salah.

Dalam ilmu logika, proposisi mempunyai tiga unsur yakni:

1. Subyek, perkara yang disebutkan adalah terdiri dari orang, benda, tempat, atau perkara.
2. Predikat adalah perkara yang dinyatakan dalam subjek.
3. Kopula adalah kata yang menghubungkan subjek dan predikat.

Dalam makalah ini saya akan menjelaskan macam-macam yang ada didalam proposisi.

1.2 Rumusan Masalah

1. Apa yang dimaksud konsep dan notasi dasar?

2. Apa saja proposisi dan tabel kebenaran?

3. Apa saja tautologi dan kontradiksi?

4. Apa saja evikalen logika?

5. Apa saja aljabar proposisi?

6. Apa saja implikasi logik?

7. Apa saja fungsi proposisi dan himpunan kebenaran?

8. Apa saja pengukur jumlah universal? contohnya negasi lingkaran.

1.3 Tujuan Penulisan

1. Untuk mengetahui pengertian konsep dan notasi dasar

2. Untuk mengetahui proposisi dan tabel kegunan

3. Untuk mengetahui tautologi dan kontradikasi

4. Untuk mengetahui ekivalen logika

5. Untuk mengetahui aljabar proposisi

6. Untuk mengetahui implikasi logika

7. Untuk mengetahui fungsi proposisi dan himpunan keturunan

8. Untuk mengetahui pengukur jumlah universal seperti contohnya negasi lingkaran

BAB 2

PEMBAHASAN

2.1 Pengertian konsep dan notasi dasar

Di dalam matematika, tidak semua kalimat berhubungan dengan logika. Hanya kalimat yang bernilai benar atau salah saja yang digunakan dalam penalaran. Kalimat tersebut dinamakan proposisi (preposition).

Proposisi adalah kalimat deklaratif yang bernilai benar (true) atau salah (false), tetapi tidak dapat sekaligus keduanya. Kebenaran atau kesalahan dari sebuah kalimat disebut nilai kebenarannya (truth value).

Contoh berikut ini dapat mengilustrasikan kalimat yang merupakan proposisi dan mana yang bukan.

Contoh 1.1

a)    6 adalah bilangan genap

b)    Soekarno adalah Presiden Indonesia yang pertama

c)    2 + 2 = 4

d)    Ibukota Provinsi Jawa Barat adalah Semarang

e)    12 ≥ 19

f)     Kemarin hari hujan

g)    Suhu di permukaan laut adalah 21 derajat celcius

h)   Pemuda itu tinggi

i)     Kehidupan hanya ada di Planet Bumi

Semuanya merupakan proposisi. Proposisi a, b, c bernilai benar, tetapi proposisi d salah karena ibukota Jawa Barat seharusnya Bandung dan proposisi e bernilai salah karena seharusnya 12 ≤ 19. Proposisi f sampai I memang tidak dapat langsung ditetapkan kebenarannya, namun satu hal yang pasti, proposisi-proposisi tersebut tidak mungkin benar dan salah sekaligus. Kita bisa menetapkan nilai proposisi tersebut benar atau salah. Misalnya, proposisi f bias kita andaikan benar (hari kemarin memang hujan) atau salah (hari kemarin tidak hujan). Demikian pula halnya untuk proposisi g dan h. Proposisi i bias benar atau salah, karena sampai saat ini belum ada ilmuwan yang dapat memastikan kebenarannya.

Contoh 1.2

a)    Jam berapa kereta api Argo Bromo tiba di Gambir?

b)    Serahkan uangmu sekarang!

c)    x + 3 = 8

d)    x > 3

bukan proposisi. Kalimat a adalah kalimat Tanya, sedangkan kalimat b adalah kalimat perintah, keduanya tidak mempunyai nilai kebenaran. Dari contoh 1.1 dan 1.2 di atas, dapat disimpulkan bahwa proposisi selalu dinyatakan sebagai kalimat berita, bukan sebagai kalimat Tanya maupun kalimat perintah. Kalimat c dan d bukan proposisi karena kedua kalimat tersebut tidak dapat ditentukan benar maupun salah sebab keduanya mengandung peubah (variable) yang tidak dispesifikasikan nilainya. Tetapi kalimat

“Untuk sembarang bilangan bulat n ≥ 0, maka 2n adalah bilangan genap”

Bidang logika yang membahas proposisi dinamakan kalkulus proposisi(propositional calculus) atau logika proposisi (propositional logic).

Secara simbolik, proposisi biasanya dilambangkan dengan huruf kecil sepertip, q, r, …. misalnya,

p: 6 adalah bilangan genap,

Untuk mendefinisikan p sebagai proposisi “6 adalah bilangan genap”. Begitu juga untuk

q : soekarno adalah Presiden Indonesia yang pertama.

r : 2 + 2 = 4.

dan sebagainya.

2.2 Tabel kebenaran dan proposisi

Tabel Kebenaran (Truth Table) adalah alat atau tabel yang digunakan untuk memberikan nilai dengan aturan tertentu.  Tabel kebenaran menunjukkan secara sistematis satu demi satu nilai-nilai kebenaran sebagai hasil kombinasi dari proposisi-proposisi yang sederhana.

Untuk melengkapi tabel kebenaran proposisi, terlebih dahulu kita harus mengetahui berapa banyak pernyataan yang termuat yang berlainan dalam tabel itu.  Langkah ini mutlak diperlukan agar tidak ada kemungkinan komposisi nilai kebenaran yang mungkin tak tertuliskan.

2.3 Tautologi dan kontradiksi

TAUTOLOGI

Tautologi adalah pernyataan majemuk yang selalu bernilai benar.

contoh pernyataan tautologi adalah:

(p ʌ q) => q

untuk membuktikan pernyataan diatas adalah tautologi, simak tabel kebenaran untuk tautologi

(p ʌ q) => q berikut;

KONTRADIKSI

Kontradiksi adalah pernyataan majemuk yang selalu bernilai salah.

contoh pernyataan kontradiksi:

 p ʌ (~p ʌ q)

tabel kebenaran pernyataan kontradiksi  p ʌ (~p ʌ q):

2.4 Ekivalen logika

Dua atau lebih pernyataan majemuk yang mempunyai nilai kebenaran sama disebut ekuivalensi logika dengan notasi “  dua buah pernyataan majemuk dikatakan ekuivalen, jika kedua pernyataan majemuk itu mempunyai nilai kebenaran yang sama untuk semua kemungkinan nilai kebenaran pernyataan-pernyataan komponen-komponennya.

Hukum-Hukum Ekuivalensi Logika:

1.   Hukum komutatif:

p ʌ q  q ʌ p

p v q q v p

2. Hukum asosiatif:

(p ʌ q) ʌ r  p ʌ (q ʌ r)

(p v q) v r  p v (q v r)

3.Hukum distributif:

p ʌ (q v r)  (p ʌ q) v (p ʌ r)

p v (q ʌ r)  (p v q) ʌ (p v r)

4. Hukum identitas:

p ʌ T  p

p v F  p 

5. Hukum ikatan (dominasi):

P v T  T

P v F  F

6. Hukum negasi:

P v ~p  T

P ʌ ~p  F

7. Hukum negasi ganda (involusi):

~(~p)  p

8. Hukum idempoten:

P ʌ p  p

p v p  p

9.  Hukum de morgan:

~( p ʌ q)  ~p v ~q

~(p v q)  ~p ʌ ~q

10. Hukum penyerapan (absorpsi):

p v (P ʌ q)  p

P ʌ (p v q)  p

11.  Hukum T dan F:

~T  F

~F  T

12.  Hukum implikasi ke and/or:

P  q  ~p v q[5]

Dengan adanya hukum-hukum diatas, penyelesaian soal-soal baik yang bersifat tautologi, kontradiksi dan ekuivalensi logika tidak hanya menggunakan tabel kebenaran namun juga bisa dengan menggunakan jalan penurunan yaitu dengan memanfaatkan 12 (dua belas) hukum-hukum ekuivalensi logika tersebut.

Dengan menggunakan prinsip-prinsip di atas, maka kalimat-kalimat yang kompleks dapat disederhanakan, seperti contoh berikut:

1.      Buktikan ekuivalensi berikut: ~(p v ~q) v (~p ʌ ~q)  ~p

Jawab:

~(p v ~q) v (~p ʌ ~q)  (~p ʌ q) v (~p ʌ ~q)

                                     ~p ʌ (q v ~q)

                                     ~p ʌ T

                                     ~p ...........(terbukti)

2.      Tunjukkan bahwa:  ~(p v q)  (~p ʌ ~q)

Tabel kebenaran ~(p v q) dan (~p ʌ ~q) yaitu:

p	q	~p	~q	p v q	~(p v q)	(~p ʌ ~q)
B B S S	B S B S	S S B B	S B S B	B B B S	S S S B	S S S B

(1)                    (2)             (3)           (4)             (5)                   (6)                        (7)  

Dari tabel diatas pada kolomk (6) dan (7), jelas bahwa ~(p v q)  (~p ʌ ~q).

Jadi, ~(p v q)  (~p ʌ ~q). 

2.5 Aljabar Proposisi

Setiap proposisi yang saling ekivalen dapat dipertukarkan atau diganti antara satu dengan yang lainnya. Di bawah ini disajikan daftar aturan penggantian untuk keperluan deduksi.

1. Hukum Idempoten (Idem)

    a. p∨q ek p

    b. p∧p ek p

2. Hukum Asosiatif (As)

    a. (p∨q)∨r ek p∨(q∨r)

    b. (p∧q)∧r ek p∧(q∧r)

3. Hukum  Komutatif (Kom)

    a. p∨q ek q∨p

    b. p∧q ek q∧p

4. Hukum Distributif (Dist)

    a. p∨(q∧r) ek (p∨q)∧(p∨r)

    b. p∧(q∨r) ek (p∧q)∨(p∧r)

5. Hukum Identitas (Id)

    a. p∨F ek p

    b. p∨T ek T

    c. p∧F ek F

    d. p∧T ek p

6. Hukum Komplemen (Komp)

    a. p∨∼p ek T

    b. p∧∼p ek F

    c. ∼(∼p) ek p

    d. ∼T ek F

7. Hukum Transposisi (Trans)

    p⇒q ek ∼q⇒∼p

8. Hukum Implikasi (Imp)

    p⇒q ek ∼p∨q

9. Hukum Ekivalensi (Eki)

    a. p⇔q ek (p⇒q)∧(q⇒p)

    b. p⇔q ek (p∧q)∨(∼q∧∼p)

10. Hukum Eksportasi (Eksp)

      (p∧q)⇒r ek p⇒(q⇒r)

11. Hukum De Morgan (DM)

       a. ∼(p∨q) ek ∼p∧∼q

       b. ∼(p∧q) ek ∼p∨∼q

2.6 Implikasi logika

Untuk memahami implikasi, pelajarilah uraian berikut. Misalnya, Elzan berjanji pada Gusrayani, “Jika Sore nanti tidak hujan, maka saya akan mengajakmu nonton”. Janji Elzan ini hanyalah berlaku untuk kondisi sore nanti tidak hujan. Akibatnya, jika sore nanti hujan, tidak ada keharusan bagi Elzan untuk mengajak Gusrayani nonton.

Misalkan sore ini tidak hujan dan Elzan mengajak Gusrayani nonton, Gusrayani tidak akan kecewa karena Elzan memenuhi janjinya. Akan tetapi, jika sore ini hujan dan Elzan tetap mengajak Gusrayani menonton, Gusrayani tentu merasa senang sekali. Jika sore ini hujan dan Elzan tidak mengajak Gusrayani menonton, tentunya Gusrayani akan memakluminya. Bagaimana jika sore ini tidak hujan dan Elzan tidak mengajak Gusrayani menonton? Itu akan lain lagi ceritanya. Tentu saja Gusrayani akan kecewa dan menganggap Elzan sebagai pembohong yang tidak menepati janjinya.

Misalkan,   p : Sore tidak hujan.

q : Elzan mengajak Gusrayani menonton.

Pernyataan “jika sore nanti tidak hujan, maka Elzan akan mengajak Gusrayani nonton”. Dapat dinyatakan sebagai “jika p maka q” atau dilambangkan dengan “p 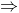 q”. Suatu pernyataan majemuk dengan bentuk “jika p maka q” disebutimplikasi.

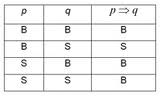
Misalkan p dan q adalah pernyataan. Suatu implikasi (pernyataan bersyarat) adalah suatu pernyataan majemuk dengan bentuk “jika p maka q”, dilambangkan dengan  p 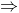  q. Pernyataan p disebut hipotesis (ada juga yang menamakananteseden) dari implikasi. Adapun pernyataan q disebut konklusi (atau kesimpulan, dan ada juga yang menamakankonsekuen). Implikasi bernilai salah hanya jika hipotesis p bernilai benar dan konklusi q bernilai salah; untuk kasus lainnya adalah benar. Perhatikan tabel berikut ini.

Tabel nilai kebenaran operasi implikasi

Terdapat perbedaan antara implikasi dalam keseharian dan implikasi dalam logika matematika. Dalam keseharian, pernyataan hipotesis/anteseden p haruslah memiliki hubungan dengan  pernyataan konklusi/konsekuen q. Misalnya, pada contoh implikasi sebelumnya, “Jika sore nanti tidak hujan maka saya akan mengajakmu nonton”. Terdapat hubungan sebab-akibat. Dalam logika matematika, pernyataan hipotesis/anteseden p tidak harus memiliki hubungan dengan konklusi/konsekuen q. Untuk lebih jelasnya, perhatikan Contoh dibawah ini.

Contoh:

Tentukanlah nilai kebenaran dari implikasi berikut !

a. Jika 4 + 7 = 10 maka besi adalah benda padat.

b. Jika 6 + 9 = 15 maka besi adalah benda cair.

c. Jika cos 30° = 0,5 maka 25 adalah bilangan ganjil.

Jawab :

a.   Jika 4 + 7 = 10 maka besi adalah benda padat.

Alasan salah, kesimpulan benar. Jadi, implikasi bernilai benar.

b.   Jika 6 + 9 = 15 maka besi adalah benda cair.

Alasan benar, kesimpulan salah. Jadi implikasi bernilai salah.

c.     Jika cos 30°= 0,5 maka 25 adalah bilangan ganjil.

Alasan salah, kesimpulan salah. Jadi, implikasi bernilai benar.

2.7 Fungsi proposisi dan himpunan keturunan

PROPOSISI DAN HIMPUNAN KEBENARAN

Proposisi merupakan penyataan yang dapat bernilai benar atau salah, tetapi tidak kedua-duanya.

Contoh: 1. Bulan terbuat dari keju ( pernyataan ini salah karna bulan tidak 

terbuat dari keju).

2. Empat adalah bilangan prima (pernyatan ini salah karna bialngan prima 

merupakan bilangan yang tidak bisa dibagi, dengan dirinya sendiri atau 

dengan bilangan lain).

3. 3 + 3 = 6 ( pernyataan ini benar karena 3 + 3 hasilnya adalah 6)

4. 2 adalah bilangan integer genap dan 3 bukan bialangan integer genap.

( pernyataan ini benar karna 2 memang bilangan genap, sedangkan 3 

adalah bilangan ganjil).

2.8 Penguruan jumlah proposisi

Negasi lingkaran

~P

Dibaca negasi P/bukan P

contoh:

1.P=7 adalah bilangan prima (B)

   ~P=7 adalah bukan bilangan prima (S)

2.q=banjarmasin adalah ibu kota kal-bar (S)

   ~ q=banjarmasin adalah bukan ibu kota kal-bar (B)

3.s:air adalah zat cair (B)

   ~ s:air adalah bukan zat cair (S)

4.r:semua burung bisa terbang (S)

    ~r:tidak semua burung bisa terbang (B)

*tabel kebenaran

P	P
B	S
S	B

*Disjungsi

            Disjungsi adalah 2 pernyataan yang dirangkai dengan kata hubung “ATAU”

pVq

Dibaca : p atau q

*rangkaian listriik:

*tabel kebenaran

p	q	Pvq
B	B	B
B	S	B
S	B	B
S	S	S

Sumber;

https://muthiashri.wordpress.com/2014/04/29/artikel-16/

http://electrica.blog.unsoed.ac.id/2010/09/24/tabel-kebenaran-proposisi/

http://hyperpost.blogspot.co.id/2014/10/logika-informatika-tentang-tautologi.html

http://dedekyohana93.blogspot.co.id/2012/11/tautologi-kontradiksi-dan-ekuivalensi_4667.html

http://princesza-vietha.blogspot.co.id/2011/10/hukum-hukum-aljabar-proposisi-aturan.html

https://smartblogmathematic.wordpress.com/ingkaran/

http://shielviarifahti.blogspot.co.id/2013/03/lingkaran-negasi.html